- Python solves problems.
- Those solutions are simple to understand.
- The code produced is simple to maintain.
Saturday, July 21, 2007
Python makes simple solutions.
The title is a slogan I thought of to counter those who say Python is simple. My slogan emphasises that :
Wednesday, July 11, 2007
I've been Crunched!
There is a new crunchy out. I just downloaded the release, unzipped to a directory, then double-clicked crunchy.py, and Firefox opened a new page of delight. Five minutes of reading and I was able to open this very blog and have all the Python code come alive. On this entry, I was able to re-run the example and have new times printed - in the browser, with just a click of an (added) button!
If I had a new algorithm I could have used the edit window supplied to write and test it as well as save my changes.
Here is what a crunchy version of this page looks like.
The added editor comes pre-loaded with my example code. The new execute button, when clicked inserts the output of running the code from the editor below it. (click on the image for a larger view).
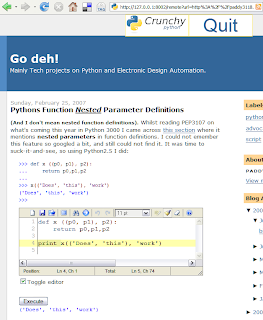
Neat!
If I had a new algorithm I could have used the edit window supplied to write and test it as well as save my changes.
Here is what a crunchy version of this page looks like.
The added editor comes pre-loaded with my example code. The new execute button, when clicked inserts the output of running the code from the editor below it. (click on the image for a larger view).

Neat!
Sunday, July 01, 2007
bit twiddling extras
As a follow up to this
I commented on what I thought would be a better solution. Richard Jones pointed us at how pyglet solved how to find the net power of two and how to check if a number is a power of two using some nifty bit twiddling.
Will McGugan then timed
both his and pyglets code, but didn't implement my suggestion (I didn't give code).
I have added an implementation of my suggestion and timed all three sets.
The timing shows that although my implementation of is_power_of_2 is fastest by a smidgen; My implementation of next_power_of_2 by iterative comparison of a list is half way between Wills and pyglets implementation, with pyglet the winner.
I have not got timings with psyco.
The code
The Timings
I commented on what I thought would be a better solution. Richard Jones pointed us at how pyglet solved how to find the net power of two and how to check if a number is a power of two using some nifty bit twiddling.
Will McGugan then timed
both his and pyglets code, but didn't implement my suggestion (I didn't give code).
I have added an implementation of my suggestion and timed all three sets.
The timing shows that although my implementation of is_power_of_2 is fastest by a smidgen; My implementation of next_power_of_2 by iterative comparison of a list is half way between Wills and pyglets implementation, with pyglet the winner.
I have not got timings with psyco.
The code
setup_1 = """
from math import log, ceil
def is_power_of_2(n):
return log(n, 2) % 1.0 == 0.0
def next_power_of_2(n):
return (2 ** ceil(log(n, 2)))
"""
setup_2 = """
def next_power_of_2(v):
v -= 1
v |= v >> 1
v |= v >> 2
v |= v >> 4
v |= v >> 8
v |= v >> 16
return v + 1
def is_power_of_2(v):
return (v & (v - 1)) == 0
"""
setup_3 = """
list_of_powers = [x**2 for x in range(32)]
set_of_powers = set(list_of_powers)
def next_power_of_2(v):
for x in list_of_powers:
if x >= v: return x
def is_power_of_2(n):
return n in set_of_powers
"""
from timeit import Timer
t1 = Timer("is_power_of_2(128)", setup_1)
t2 = Timer("is_power_of_2(128)", setup_2)
t3 = Timer("next_power_of_2(125)", setup_1)
t4 = Timer("next_power_of_2(125)", setup_2)
t5 = Timer("is_power_of_2(128)", setup_3)
t6 = Timer("next_power_of_2(125)", setup_3)
print "float math is_power_of_2:", t1.timeit()
print "bit-twiddling is_power_of_2:", t2.timeit()
print "set-lookup is_power_of_2:", t5.timeit()
print "float math next power of 2:", t3.timeit()
print "bit-twiddling next power of 2:", t4.timeit()
print "list-comparison next power of 2:", t6.timeit()
The Timings
float math is_power_of_2: 2.33588961726
bit-twiddling is_power_of_2: 0.573784377623
set-lookup is_power_of_2: 0.54499859619
float math next power of 2: 3.06279429369
bit-twiddling next power of 2: 2.08060354039
list-comparison next power of 2: 2.58548279181