- Create an empty list
- then for each node starting at the root which has a depth of zero:
- add the (depth, name) tuple of the node to the list
- visit all this nodes child node.
An example tree:
Its indent format:
[(0, 'R'), (1, 'a'), (2, 'c'), (3, 'd'), (3, 'h'), (1, 'b'), (2, 'e'), (3, 'f'), (4, 'g'), (2, 'i')]
Indented representation:
If you print out successive names from the indent format list above, one per line, with indent from the left of the indent value, then you get a nice textual regpresentation of the tree; expanded left-to-right rather than the top-down representation of the graphic:R
a
c
d
h
b
e
f
g
i
Code
I wrote some code to manipulate and traverse this kind of tree datastructure, as well as to use graphviz to draw graphical representations.1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 | import graphviz as gv from collections import defaultdict import re from pprint import pprint as pp #%% node_attr = {at: val for at, val in (line.strip().split() for line in ''' shape record fontsize 12 height 0.1 width 0.1 rankdir LR ranksep 0.25 nodesep 0.25 '''.strip().split('\n'))} edge_attr = {at: val for at, val in (line.strip().split() for line in ''' arrowhead none minlen 1 '''.strip().split('\n'))} root_attr = {at: val for at, val in (line.strip().split() for line in ''' fontcolor green color brown fontname bold '''.strip().split('\n'))} #%% def _pc2indent(pc, root=None, indent=None, children=None): "parent-child dependency dict to indent format conversion" if root is None: parents = set(pc) kids = set(sum(pc.values(), [])) root = parents - kids assert len(root) == 1, f"Need exactly one root: {root}" root = root.pop() if indent is None: indent = 0 if children is None: children = [] children.append((indent, root)) if root in pc: for child in pc[root]: pc2indent(pc, child, indent+1, children) return children def dot2indent(tree): "simple dot format to indent format translator" depends = defaultdict(list) for matchobj in re.finditer(r'\s+(\S+)\s*->\s*(\S+)\s', tree.source): parent, child = matchobj.groups() depends[parent].append(child) parent2child = dict(depends) return _pc2indent(parent2child) #%% def _highlight(txt): return f'#{txt}#' def pp_indent(data, hlight=None, indent=' '): "simple printout of indent format tree with optional node highlighting" if hlight is None: hlight = set() for level, name in data: print(indent * level + (_highlight(name) if name in hlight else name)) #%% def indent2dot(lst): tree = gv.Digraph(name='indent2dot', node_attr=node_attr) tree.edge_attr.update(**edge_attr) levelparent = {} for level, name in lst: levelparent[level] = name if level - 1 in levelparent: tree.edge(levelparent[level-1], name) else: tree.node(name, _attributes=root_attr) return tree #%% def printwithspace(i): print(i, end=' ') def preorder(tree, visitor=printwithspace): for indent, name in tree: visitor(name) def levelorder(tree, reverse_depth=False, reverse_in_level=False, visitor=printwithspace): if not tree: return indent2name = defaultdict(list) mx = -1 for indent, name in tree: if indent > mx: mx = indent indent2name[indent].append(name) if reverse_in_level: for names in indent2name.values(): names.reverse() if not reverse_depth: for indent in range(0, mx + 1): for name in indent2name[indent]: visitor(name) else: for indent in range(mx, -1, -1): for name in indent2name[indent]: visitor(name) #%% # Example tree ex1 = [(0, '1'), (1, '2'), (2, '4'), (3, '7'), (2, '5'), (1, '3'), (2, '6'), (3, '8'), (3, '9'), (3, '10'), ] #%% if __name__ == '__main__': print('A tree in indent datastructure format:') pp(ex1) print('\nSame tree, printed as indented list:') pp_indent(ex1) print('\nSame tree, drawn by graphviz:') display(indent2dot(ex1)) # display works in spyder/Jupyter print('\nSame tree, preorder traversal:') preorder(ex1) print() print('Same tree, levelorder traversal:') levelorder(ex1) print() print('Same tree, reverse_depth levelorder traversal:') levelorder(ex1, True) print() print('Same tree, reverse_depth, reverse_in_level levelorder traversal:') levelorder(ex1, True, True) print() print('Same tree, depth_first, reverse_in_level levelorder traversal:') levelorder(ex1, False, True) print() |
Output:
A tree in indent datastructure format:
[(0, '1'),
(1, '2'),
(2, '4'),
(3, '7'),
(2, '5'),
(1, '3'),
(2, '6'),
(3, '8'),
(3, '9'),
(3, '10')]
Same tree, printed as indented list:
1
2
4
7
5
3
6
8
9
10
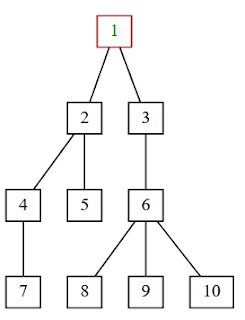
Same tree, drawn by graphviz:
Same tree, preorder traversal:
1 2 4 7 5 3 6 8 9 10
Same tree, levelorder traversal:
1 2 3 4 5 6 7 8 9 10
Same tree, reverse_depth levelorder traversal:
7 8 9 10 4 5 6 2 3 1
Same tree, reverse_depth, reverse_in_level levelorder traversal:
10 9 8 7 6 5 4 3 2 1
Same tree, depth_first, reverse_in_level levelorder traversal:
1 3 2 6 5 4 10 9 8 7
In [47]:

Cool and all, but what's this good for?
ReplyDeleteHmm, the indented tree layout is textand quite compact. For me, it's new and I'll add it to my datastructures toolbox for now.
Delete